有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出 的分布列,求
的分布列,求 的数学期望。
的数学期望。
如图,四棱锥 中,
中, 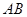 ∥
∥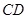 ,
,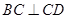 ,侧面
,侧面 为等边三角形.
为等边三角形. .
.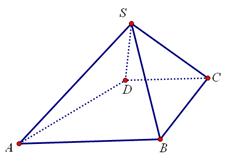
(1)证明:
(2)求AB与平面SBC所成角的正弦值。
电流强度I与时间t的关系式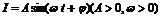 。(1)在一个周期内
。(1)在一个周期内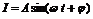 如图所示,试根据图象写出
如图所示,试根据图象写出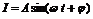 的解析式;(2)为了使
的解析式;(2)为了使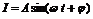 中t在任意一段
中t在任意一段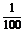 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数 的最小值为多少?
的最小值为多少?
已知
(1)化简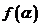 ;
;
(2)若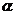 是第三象限角,且
是第三象限角,且 的值;
的值;
(3)求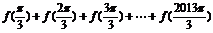 的值。
的值。
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若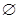
 A∩B,A∩C=
A∩B,A∩C=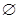 ,求a的值.
,求a的值.
已知
(1)求函数 的最小值;
的最小值;
(2)对一切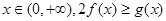 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.