已知椭圆 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证:
已知椭圆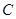 的对称中心为原点
的对称中心为原点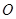 ,焦点在
,焦点在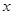 轴上,左、右焦点分别为
轴上,左、右焦点分别为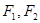 ,且
,且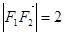 ,点
,点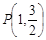 在该椭圆上.
在该椭圆上.
(1)求椭圆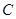 的方程;
的方程;
(2)过点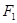 的直线
的直线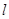 与椭圆
与椭圆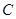 相交于
相交于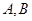 两点,若
两点,若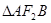 的面积为
的面积为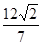 ,求以
,求以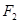 为圆心且与直线
为圆心且与直线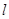 相切的圆的方程.
相切的圆的方程.
在三棱柱 中,侧面
中,侧面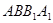 为矩形,
为矩形,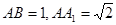 ,
,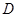 为
为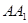 的中点,
的中点,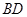 与
与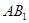 交于点
交于点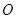 ,
,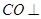 侧面
侧面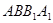 .
.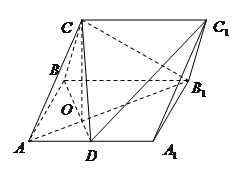
(1)证明: ;
;
(2)若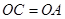 ,求三棱柱
,求三棱柱 的体积.
的体积.
正项数列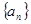 前
前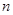 项和
项和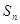 满足
满足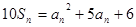 且
且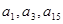 成等比数列,求
成等比数列,求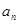 .
.
如图,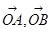 为平面的一组基向量,
为平面的一组基向量,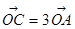 ,
,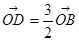 ,
, 与
与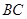 交与点
交与点

(1)求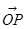 关于
关于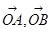 的分解式;(2)设
的分解式;(2)设 ,
, ,求
,求 ;
;
(3)过 任作直线
任作直线 交直线
交直线 于
于 两点,设
两点,设
 ,
,
( )求
)求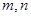 的关系式。
的关系式。
已知对任意平面向量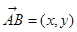 ,把
,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量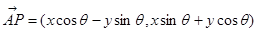 ,叫做把点
,叫做把点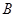 绕点
绕点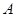 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。
(1)已知平面内点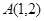 ,点
,点 。把点
。把点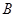 绕点
绕点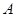 沿逆时针旋转
沿逆时针旋转 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;
(2)设平面内直线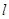 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转 后得到的点组成的直线方程是
后得到的点组成的直线方程是 ,求原来的直线
,求原来的直线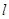 方程。
方程。