已知动圆M过定点P(0,m)(m>0),且与定直线 相切,动圆圆心M的轨迹方程为C,直线
相切,动圆圆心M的轨迹方程为C,直线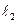 过点P 交曲线C于A、B两点。
过点P 交曲线C于A、B两点。
(1)若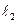 交
交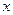 轴于点S,求
轴于点S,求 的取值范围;
的取值范围;
(2)若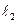 的倾斜角为
的倾斜角为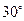 ,在
,在 上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.
上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.
(满分10分)已知定义在 上的函数
上的函数 其中
其中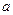 为常数。
为常数。
(1)若 是函数
是函数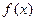 的一个极值点,求
的一个极值点,求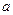 的值;
的值;
(2)若函数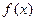 在区间
在区间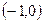 上为增函数,求
上为增函数,求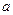 的取值范围
的取值范围
(满分10分)设函数
(1) 当 时,求函数
时,求函数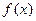 的极
的极 值;
值;
(2) 当 时,求函数
时,求函数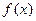 在定义域内的单调性.
在定义域内的单调性.
..(满分8分)已知数列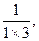
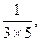

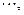
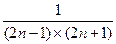 ,
,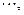
(1)计算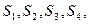
(2)根据(1)的计算结果,猜想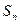 的表达式
的表达式 ,并用数学归纳法进行证明。
,并用数学归纳法进行证明。
(满分8分)已知 名学生和
名学生和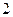 名教师站在一排照相,(用数字作答)求:
名教师站在一排照相,(用数字作答)求:
(1)中间二个位置排教师,有多少种排法?
(2) 首尾不排教师,有多少种排法?
首尾不排教师,有多少种排法?
(3)两名教师不能相邻的排法有多少种?
(本小题满分10分)
已知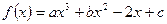 在
在 时有极大值6,在
时有极大值6,在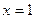 时有极小值.
时有极小值.
(Ⅰ)求 的值;
的值;
(Ⅱ)求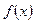 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.