如图3,在直三棱柱ABC—A1B1C1中,AB1⊥BC1,AB=CC1=1,BC=2.
(1)求证:A1C1⊥AB;
(2)求点B1到平面ABC1的距离.
(本小题满分10分)选修4-1 :几何证明选讲
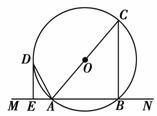
直线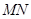 交圆
交圆 于
于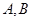 两点,
两点,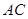 是直径,
是直径,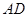 平分
平分 ,交圆
,交圆 于点
于点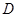 ,过
,过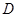 作
作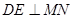 于
于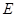 。
。
(Ⅰ)求证: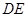 是圆
是圆 的切线;
的切线;
(Ⅱ)若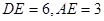 ,求
,求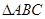 的面积。
的面积。
(本小题满分12分)已知函数 ,
,
(Ⅰ)求函数 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对任意的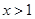 ,恒有
,恒有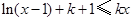 成立,求
成立,求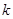 的取值范围;
的取值范围;
(Ⅲ)证明: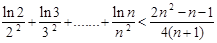 (
(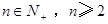 ).
).
(本小题满分12分)已知椭圆C: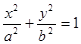 (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为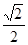 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
(本小题满分12分)如图,四棱锥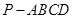 ,侧面
,侧面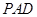 是边长为
是边长为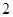 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面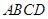 是
是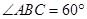 的菱形,
的菱形, 为
为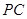 的中点.
的中点.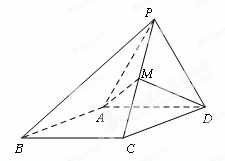
(Ⅰ)求证: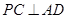 ;
;
(Ⅱ)求点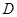 到平面
到平面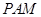 的距离.
的距离.
(本小题满分12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| “厨余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为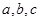 ,其中
,其中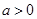 ,
, .当数据
.当数据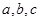 的方差
的方差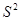 最大时,写出
最大时,写出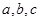 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时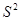 的值.(注:方差
的值.(注:方差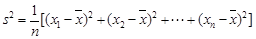 ,其中
,其中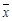 为
为 的平均数)
的平均数)