某校组织一次冬令营活动，有8名同学参加，其中有5名男同学，3名女同学，为了活动的需要，要从这8名同学中随机抽取3名同学去执行一项特殊任务，记其中有X名男同学.
（1）求X的概率分布；
（2）求去执行任务的同学中有男有女的概率.
某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为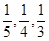
（各学校是否录取他相互独立，允许他可以被多个学校同时录取）.
（Ⅰ）求此同学没有被任何学校录取的概率；
（Ⅱ）求此同学至少被两所学校录取的概率.
下表是关于宿州市服装机械厂某设备的使用年限
（年）和所需要的维修费用
（万元）的几组统计数据：
|
2 |
3 |
4 |
5 |
6 |
|
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
（Ⅰ）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；
（Ⅱ）估计使用年限为10年时，维修费用为多少？
（参考：（1）
（2）
）
已知
，求证：
.
实数
取什么数值时，复数
分别是：
（Ⅰ）实数；（Ⅱ）纯虚数.
设函数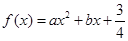
在
处取得极值，且曲线
在点
处的切线垂直于直线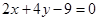
.
(Ⅰ) 求
的值；
（Ⅱ）求曲线和直线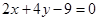所围成的封闭图形的面积；
（Ⅲ）设函数
，若方程
有三个不相等的实根，求
的取值范围.