如图1,在边长为 的正三角形
的正三角形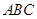 中,
中, ,
, ,
, 分别为
分别为 ,
,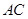 ,
,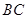 上的点,且满足
上的点,且满足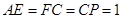 .将△
.将△ 沿
沿 折起到△
折起到△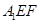 的位置,使二面角
的位置,使二面角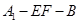 成直二面角,连结
成直二面角,连结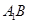 ,
,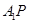 .(如图2)
.(如图2)
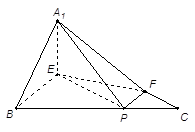
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求直线 与平面
与平面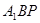 所成角的大小.
所成角的大小.
设函数 ,
,
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若 ,
, ,求
,求 的面积的最大值.
的面积的最大值.
已知函数 ,设
,设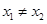 且
且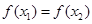 .
.
(1)证明: ,且
,且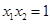 ;
;
(2)若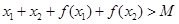 对任意满足条件的
对任意满足条件的 ,
,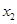 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
已知函数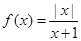 .
.
(1)求 的单调区间;
的单调区间;
(2)若方程 有四个不等实根,求实数
有四个不等实根,求实数 的取值范围.
的取值范围.
某学校假期后勤维修的一项工作是请30名木工制作200把椅子和100张课桌.已知一名工人在单位时间内可制作10把椅子或7张课桌.将这30名工人分成两组,一组制作课桌,一组制作椅子,两组同时开工.设制作课桌的工人为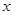 名.
名.
(1)分别用含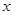 的式子表示制作200把椅子和100张课桌所需的单位时间;
的式子表示制作200把椅子和100张课桌所需的单位时间;
(2)当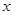 为何值时,完成此项工作的时间最短?
为何值时,完成此项工作的时间最短?
如图,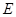 是直角梯形
是直角梯形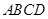 底边
底边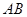 的中点,
的中点, ,将△
,将△ 沿
沿 折起形成四棱锥
折起形成四棱锥 .
.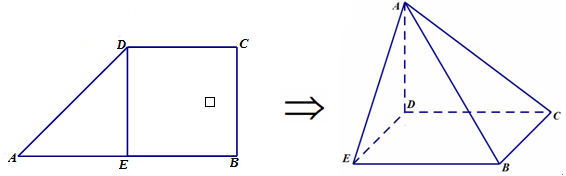
(1)求证: 平面
平面 ;
;
(2)若二面角 为
为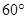 ,求二面角
,求二面角 的正切值.
的正切值.