学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分;B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
(本小题满分12分)不使用计算器,计算下列各题:
(1)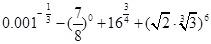 ;
;
(2) .
.
(本小题满分12分)已知函数定义域为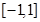 ,若对于任意的
,若对于任意的 ,都有
,都有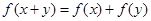 ,且时,有.
,且时,有.
(Ⅰ)证明函数是奇函数;
(Ⅱ)讨论函数在区间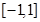 上的单调性;
上的单调性;
(Ⅲ)设,若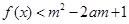 ,对所有
,对所有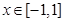 ,
,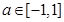 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)银川市有甲,乙两家室内羽毛球馆,两家设备和服务都相当,但收费方式不同.甲羽毛球馆每小时50元;乙羽毛球馆按月计费,一个月中30小时以内(含30小时)900元,超过30小时的部分每小时20元.肖老师为了锻炼身体,准备下个月从这两家羽毛球馆中选择一家进行健身活动,其活动时间不少于15小时,也不超过40小时.设甲羽毛球馆健身 小时的收费为
小时的收费为 元,乙羽毛球馆健身
元,乙羽毛球馆健身 小时的收费为
小时的收费为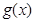 元.
元.
(Ⅰ)当 时,分别写出函数
时,分别写出函数 和
和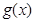 的表达式;
的表达式;
(Ⅱ)请问肖老师选择哪家羽毛球馆健身比较合算?为什么?
(本小题满分12分)已知函数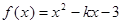 ,
,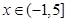 .
.
(Ⅰ)当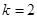 时,求函数
时,求函数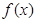 的值域;
的值域;
(Ⅱ)若函数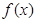 在区间
在区间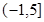 上是单调函数,求实数
上是单调函数,求实数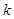 的取值范围.
的取值范围.
(本小题满分12分)已知函数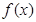 是定义在
是定义在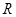 上的偶函数.若
上的偶函数.若 时,
时,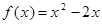 .
.
(Ⅰ)当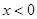 时,求函数
时,求函数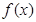 的解析式;
的解析式;
(Ⅱ)画出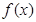 的简图;(要求绘制在答题卷的坐标纸上);
的简图;(要求绘制在答题卷的坐标纸上);
(Ⅲ)结合图像写出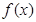 的单调区间(只写结论,不用证明).
的单调区间(只写结论,不用证明).