已知集合
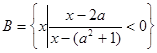 .
.
(1)当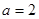 时,求
时,求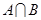 ;
;
(2)求使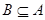 的实数
的实数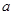 的取值范围.
的取值范围.
(本题满分13分)已知f(x)= 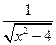 (x<-2),f(x)的反函数为g(x),点A(an,
(x<-2),f(x)的反函数为g(x),点A(an,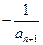 )在曲线y=g(x) (nÎN*)上,且a1=1。
)在曲线y=g(x) (nÎN*)上,且a1=1。
(Ⅰ)求y=g(x)的表达式;
(Ⅱ)证明数列{ }为等差数列。
}为等差数列。
(本题满分12分)F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.(Ⅰ)根据条件求出b和k满足的关系式;(Ⅱ)向量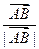 在向量
在向量 方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本题满分12分)已知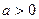 ,函数
,函数 .(1)设曲线
.(1)设曲线 在点
在点 处的切线为
处的切线为 ,若
,若 与圆
与圆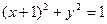 相切,求
相切,求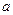 的值;(2)求函数
的值;(2)求函数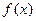 的单调区间;(3)求函数
的单调区间;(3)求函数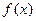 在[0,1]上的最小值。
在[0,1]上的最小值。
(本题满分13分) 已知椭圆 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过 、
、 、
、 三点.(1)求椭圆
三点.(1)求椭圆 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆 上不同于
上不同于 、
、 的任意一点,
的任意一点, ,当
,当 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线 与椭圆
与椭圆 交于
交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
棱长为4的正四面体与一个球,若球与正四面体的六条棱都相切,求这个球的体积.