已知函数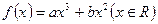
的图像过点P（-1，2），且在点P处的切线恰好与直线
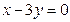垂直。
(1)求函数
的解析式；
(2)若函数在区间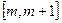
上单调递增，求实数m的取值范围。
设f(x)＝a(x－5)2＋6ln x，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线与y轴相交于点(0,6)．
(1)确定a的值；
(2)求函数f(x)的单调区间与极值．
已知函数f(x)＝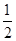
ax2－(2a＋1)x＋2ln x，a∈R.
(1)若曲线y＝f(x)在x＝1和x＝3处的切线互相平行，求a的值；
(2)求f(x)的单调区间．
已知f(x)＝ex－ax－1.
(1)求f(x)的单调增区间；
(2)若f(x)在定义域R内单调递增，求a的取值范围．
已知函数f(x)＝x2＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．
(1)证明：当x≥0时，f(x)≤(x＋c)2；
(2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c2－b2)恒成立，求M的最小值．
已知函数f(x)＝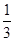
ax3－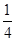
x2＋cx＋d(a，c，d∈R)满足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．
(1)求a，c，d的值；
(2)若h(x)＝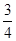
x2－bx＋
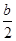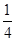－，解不等式f′(x)＋h(x)<0.