已知函数f(x)=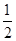 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间.
当m为参数时,集合A={(x,y)∣x2+y2+x-6y+m=0}是以(-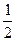 ,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
李明同学准备用100元买空白磁盘和空白光碟,已知空白磁盘售价为4元/张,空白光碟的售价7元/张,问李明同学怎样设计购买方案,才能达到磁盘、光碟都买并且都不超过10张,而又使剩下的钱最少。
已知直线l:y=k(x+2 与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
已知x2+y2=9的内接△ABC中,点A的坐标是(-3,0),重心G的坐标是(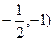 ,求(1)直线BC的方程;(2)弦BC的长度.
,求(1)直线BC的方程;(2)弦BC的长度.
已知圆心在直线2x+y=0上,且过点A(2,-1),与直线x-y-1=0相切,求圆的方程。