已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x).
(1)证明:当x≥0时,f(x)≤(x+c)2;
(2)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
(本小题满分13分)
已知椭圆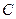 的焦点分别为
的焦点分别为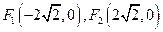 ,且过点
,且过点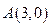 .
.
(1)求椭圆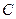 的标准方程;
的标准方程;
(2)设 为椭圆
为椭圆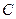 内一点,直线
内一点,直线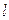 交椭圆
交椭圆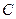 于
于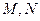 两点,且
两点,且 为线段
为线段 的中点,求直线
的中点,求直线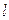 的方程.
的方程.
本小题满分13分)
先后随机投掷2枚正方体(六面分别标有 )骰子,其中
)骰子,其中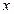 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,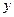 表示第
表示第 枚骰子出现的点数。
枚骰子出现的点数。
(1)求点 在直线
在直线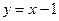 上的概率;
上的概率;
(2)求点 满足
满足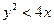 的概率。
的概率。
某工厂生产一种机器的固定成本为5000元,且每生产100部,需要增加投入2500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部。已知年销售收入为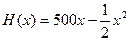 ,其中x是产品售出的数量
,其中x是产品售出的数量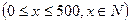 。
。
(1 )若x为年产量,y 表示年利润,求
)若x为年产量,y 表示年利润,求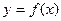 的表达式。(年利
的表达式。(年利 润=年销售收入—投资成本(包括固定成本))
润=年销售收入—投资成本(包括固定成本))
(2)当年产量为何值时,工厂的年利润最大,其最大值是多少?
解关于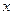 的不等式:
的不等式:
(1) 2≤|3x-2 |<8 (x
|<8 (x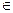 Z )(2) x2-(a+1)x+a<0,.
Z )(2) x2-(a+1)x+a<0,.
(本小题满分12分)
已知p:方程x2+mx+1=0有两个不等的 负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。
负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。