本小题满分13分)
先后随机投掷2枚正方体(六面分别标有 )骰子,其中
)骰子,其中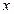 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,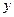 表示第
表示第 枚骰子出现的点数。
枚骰子出现的点数。
(1)求点 在直线
在直线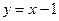 上的概率;
上的概率;
(2)求点 满足
满足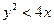 的概率。
的概率。
(本小题共10分)
三棱柱ABC—A1B1C1中,CC1⊥平面ABC,△ABC是边长为2的等边三角形,D为AB边中点,且CC1=2AB.
(1)(4′)求证:平面C1CD⊥平面ABC;
(2)(6′)求三棱锥D—CBB1的体积.
( 10分) 已知函数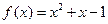
(1)(4′) 求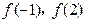
(2)(6′)求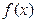 的最小值
的最小值
已知集合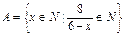 ,试用列举法表示集合
,试用列举法表示集合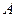

、已知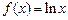 ,
,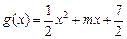 (
(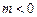 ),直线
),直线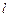 与函数
与函数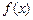 、
、 的图像都
的图像都
相切,且与函数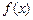 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线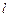 的方程及
的方程及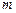 的值;
的值;
(Ⅱ)若 (其中
(其中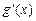 是
是 的导函数),求函数
的导函数),求函数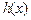 的最大值;
的最大值;
(Ⅲ)当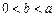 时,求证:
时,求证: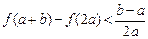 .
.
已知定点A(-1,0),F(2,0),定直线l:x= ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由