某工厂生产一种机器的固定成本为5000元,且每生产100部,需要增加投入2500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部。已知年销售收入为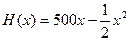 ,其中x是产品售出的数量
,其中x是产品售出的数量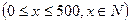 。
。
(1 )若x为年产量,y 表示年利润,求
)若x为年产量,y 表示年利润,求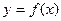 的表达式。(年利
的表达式。(年利 润=年销售收入—投资成本(包括固定成本))
润=年销售收入—投资成本(包括固定成本))
(2)当年产量为何值时,工厂的年利润最大,其最大值是多少?
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| 甲班 (A方式) |
乙班 (B方式) |
总计 |
|
| 成绩优秀 |
|||
| 成绩不优秀 |
|||
| 总计 |
附: 
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k |
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
已知二项式 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;(2)设
的值;(2)设 .
.
①求 的值; ②求
的值; ②求 的值.
的值.
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间 与零件个数
与零件个数 之间有较好的线性相关关系。(
之间有较好的线性相关关系。( )
)
 |
2 |
3 |
4 |
5 |
 |
2.5 |
3 |
4 |
4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式 )
)
已知不等式 .
.
(1)若对 不等式恒成立,求实数
不等式恒成立,求实数 的取值范围;
的取值范围;
(2)若对 不等式恒成立,求实数
不等式恒成立,求实数 的取值范围;
的取值范围;
(3)若对满足 的一切m的值不等式恒成立,求实数
的一切m的值不等式恒成立,求实数 的取值范围.
的取值范围.
(1)设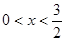 ,求函数
,求函数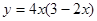 的最大值;
的最大值;
(2)已知x、y都是正实数,且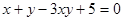 ,求
,求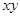 的最小值.
的最小值.