已知函数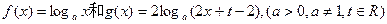 的图象在x=2处的切线互相平行.
的图象在x=2处的切线互相平行.
(1)求t的值.
(2)设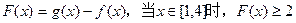 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(本小题满分14分)已知函数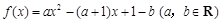 .
.
(Ⅰ)若 ,关于
,关于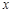 的不等式
的不等式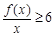 在区间
在区间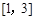 上恒成立,求
上恒成立,求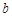 的取值范围;
的取值范围;
(Ⅱ)若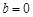 ,解关于
,解关于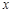 的不等式
的不等式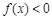 ;
;
(Ⅲ)若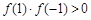 ,且
,且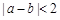 ,求
,求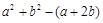 的取值范围.
的取值范围.
(本小题满分13分)已知点 ,点
,点 ,直线l:
,直线l: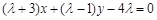 (其中
(其中 ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若直线l与线段AB有公共点,求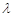 的取值范围;
的取值范围;
(Ⅲ)若分别过A,B且斜率为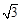 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为 ,求直线
,求直线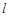 的方程.
的方程.
(本小题满分12分)在数列 中,
中, ,又
,又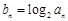 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)设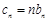 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)在△ABC中,角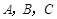 对边分别为
对边分别为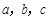 .设向量
.设向量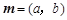 ,
, ,
,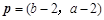 .
.
(Ⅰ)若m∥n,求证:△ABC为等腰三角形;
(Ⅱ)已知c=2, ,若m⊥p,求△ABC的面积S.
,若m⊥p,求△ABC的面积S.
(本小题满分12分)已知点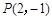 .
.
(Ⅰ)直线m经过点P,且在两坐标轴上的截距相等,求直线m的方程;
(Ⅱ)直线n经过点P,且坐标原点到该直线的距离为2,求直线n的方程.