已知抛物线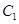 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线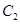 :
: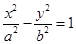 的一个焦点
的一个焦点 且垂直于
且垂直于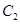 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线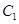 与双曲线
与双曲线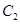 的一个交点是
的一个交点是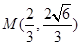 .
.
(1)求抛物线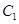 的方程及其焦点
的方程及其焦点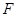 的坐标;
的坐标;
(2)求双曲线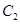 的方程及其离心率
的方程及其离心率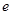 .
.
已知复数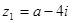 ,
,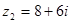 ,
,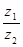 为纯虚数.
为纯虚数.
(1)求实数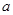 的值;(2)求复数
的值;(2)求复数 的平方根
的平方根
已知集合 ,
,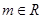 .
.
(1)若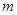 = 3,求
= 3,求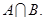 ;
;
(2)若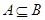 ,求实数
,求实数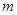 的取值范围.
的取值范围.
已知数列 的前n项和为
的前n项和为 ,且
,且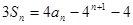
 ,令
,令 .
.
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)若
 ,用数学归纳法证明
,用数学归纳法证明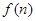 是18的倍数.
是18的倍数.
已知 展开式的二项式系数之和为256.
展开式的二项式系数之和为256.
(1)求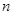 ;
;
(2)若展开式中常数项为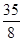 ,求
,求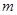 的值;
的值;
(3)若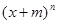 展开式中系数最大项只有第6项和第7项,求
展开式中系数最大项只有第6项和第7项,求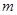 的取值情况.
的取值情况.
某地有10个著名景点,其中8 个为日游景点,2个为夜游景点.某旅行团要从这10个景点中选5个作为二日游的旅游地.行程安排为第一天上午、下午、晚上各一个景点,第二天上午、下午各一个景点.
(1)甲、乙两个日游景点至少选1个的不同排法有多少种?
(2)甲、乙两日游景点在同一天游玩的不同排法有多少种?
(3)甲、乙两日游景点不同时被选,共有多少种不同排法?