已知集合 ,
,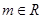 .
.
(1)若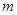 = 3,求
= 3,求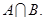 ;
;
(2)若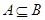 ,求实数
,求实数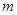 的取值范围.
的取值范围.
已知函数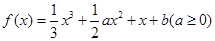 ,
, 为函数
为函数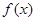 的导函数.
的导函数.
(1)设函数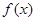 的图象与
的图象与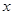 轴交点为
轴交点为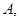 曲线
曲线 在
在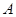 点处的切线方程是
点处的切线方程是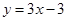 ,求
,求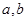 的值;
的值;
(2)若函数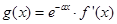 ,求函数
,求函数 的单调区间.
的单调区间.
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为 第二、第三门课程取得优秀成绩的概率分别为
第二、第三门课程取得优秀成绩的概率分别为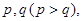 且不同课程是否取得优秀成绩相互独立,记
且不同课程是否取得优秀成绩相互独立,记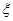 为该生取得优秀成绩的课程数,其分布列为
为该生取得优秀成绩的课程数,其分布列为
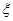 |
0 |
1 |
2 |
3 |
 |
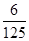 |
 |
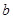 |
 |
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求 ,
,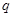 的值;
的值;
(3)求数学期望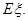
已知四棱锥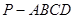 的底面
的底面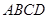 是边长为
是边长为 的正方形,
的正方形,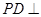 底面
底面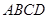 ,
,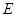 、
、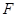 分别为棱
分别为棱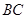 、
、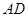 的中点.
的中点.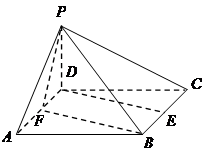
(1)求证: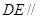 平面
平面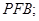
(2)已知二面角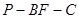 的余弦值为
的余弦值为 求四棱锥
求四棱锥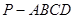 的体积.
的体积.
已知:以点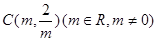 为圆心的圆与
为圆心的圆与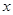 轴交于点
轴交于点 、
、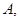 与
与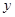 轴交于点
轴交于点 、
、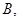 其中
其中 为原点.
为原点.
(1)求证: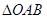 的面积为定值;
的面积为定值;
(2)设直线 与圆
与圆 交于点
交于点 、
、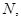 若
若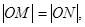 求⊙
求⊙ 的方程.
的方程.
在锐角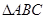 中,角
中,角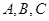 的对边分别为
的对边分别为 且
且 .
.
⑴求 的值;
的值;
⑵求 的取值范围.
的取值范围.