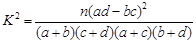某地有10个著名景点,其中8 个为日游景点,2个为夜游景点.某旅行团要从这10个景点中选5个作为二日游的旅游地.行程安排为第一天上午、下午、晚上各一个景点,第二天上午、下午各一个景点.
(1)甲、乙两个日游景点至少选1个的不同排法有多少种?
(2)甲、乙两日游景点在同一天游玩的不同排法有多少种?
(3)甲、乙两日游景点不同时被选,共有多少种不同排法?
已知直线 被两直线
被两直线 和
和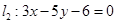 截得线段的中点为
截得线段的中点为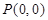 ,求直线
,求直线 的方程.
的方程.
已知函数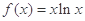 .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)若 在
在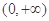 上恒成立,求实数
上恒成立,求实数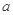 的取值范围;
的取值范围;
(3)过点 作函数
作函数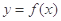 图像的切线,求切线方程.
图像的切线,求切线方程.
已知函数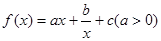 的图象在点(1,
的图象在点(1,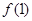 )处的切线方程为
)处的切线方程为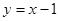 。
。
(1)用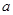 表示出
表示出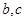 ;
;
(2)若 在[1,+∞)上恒成立,求
在[1,+∞)上恒成立,求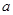 的取值范围.
的取值范围.
已知
(1)讨论 的单调性;
的单调性;
(2)当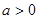 时,若对于任意
时,若对于任意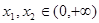 ,都有
,都有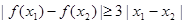 ,求
,求 的取值范围.
的取值范围.
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽查了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.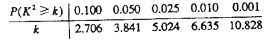
| 月收入(单位百元) |
[15,25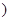 |
[25,35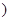 |
[35,45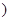 |
[45,55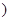 |
[55,65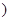 |
[65,75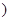 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
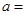 |
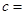 |
|
| 不赞成 |
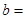 |
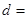 |
|
| 合计 |
(2)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取1人进行追踪调查,求选中的2人中不赞成“楼市限购令”人数至多1人的概率。
参考数据: