已知A,B,C,D四个城市,它们各自有一个著名的旅游点,依次记为A,b,C,D,把A,B,C,D和A,b,C,D分别写成左、右两列.现在一名旅游爱好者随机用4条线把城市与旅游点全部连接起来, 构成“一一对应”.规定某城市与自身的旅游点相连称为“连对”,否则称为“连错”,连对一条得2分,连错一条得0分.
(Ⅰ)求该旅游爱好者得2分的概率.
(Ⅱ)求所得分数 的分布列和数学期望.
的分布列和数学期望.
为考虑广告费用x与销售额y之间的关系,抽取了5家餐厅,得到如下数据:
| 广告费用(千元) |
1.0 |
4.0 |
6.0 |
10.0 |
14.0 |
| 销售额(千元) |
19.0 |
44.0 |
40.0 |
52.0 |
53.0 |
(1)在同一张图上画散点图,直线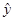 (1)=24+2.5x,
(1)=24+2.5x,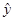 (2)=
(2)=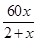 ;
;
(2)比较所画直线与曲线,哪一条更能表现这组数据之间的关系?
(3)分别计算用直线方程与曲线方程得到在5个x点处的销售额预测值、预测值与实际预测之间的误差,最后比较两个误差绝对值之和的大小。
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如图所示.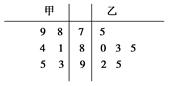
从平均成绩及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
| 分组 |
频数 |
频率 |
|
| 一组 |
0≤t<5 |
0 |
0 |
| 二组 |
5≤t<10 |
10 |
0.10 |
| 三组 |
10≤t<15 |
10 |
② |
| 四组 |
15≤t<20 |
① |
0.50 |
| 五组 |
20≤t≤25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
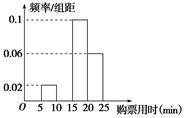
解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: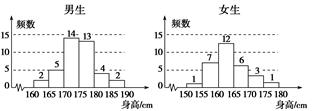
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185 cm之间的概率.
甲、乙两篮球运动员上赛季每场比赛的得分如下:
甲:12,15,24,25,31,31,36,36,37,39,44,49,50;
乙:8,13,14,16,23,26,27,33,38,39,51.
试比较这两位运动员的得分水平.