(本小题满分13分)已知甲、乙、丙三种食物的维生素A、B含量及成本如下表:
| |
甲 |
乙 |
丙 |
| 维生素A(单位/kg) |
60 |
70 |
40 |
| 维生素B(单位/kg) |
80 |
40 |
50 |
| 成本(元/kg) |
11 |
9 |
4 |
现分别用甲、乙、丙三种食物配成10kg混合食物,并使混合食物内至少含有560单位维生素A和630单位维生素B.
(Ⅰ)若混合食物中恰含580单位维生素A和660单位维生素B,求混合食物的成本为多少元?
(Ⅱ)分别用甲、乙、丙三种食物各多少kg,才能使混合食物的成本最低?最低成本为多少元?
已知数列 为等差数列,且
为等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)证明 …
… .
.
已知 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的
的
不等式 的解集是空集。
的解集是空集。
(1)求角 的最大值;
的最大值;
(2)若 ,
, 的面积
的面积 ,求当角
,求当角 取最大值时
取最大值时 的值。
的值。
已知向量 ,
, =(
=( ,
, ),记
),记 ;
;
(1)若 ,求
,求 的值;
的值;
(2)若 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
在海岸 处,发现北偏东
处,发现北偏东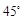 方向,距
方向,距 为
为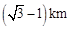 的
的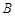 处有一艘走私船,在
处有一艘走私船,在 处北偏西
处北偏西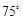 方向,距
方向,距 为
为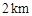 的
的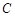 处的缉私船奉命以
处的缉私船奉命以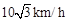 的速度追截走私船,此时走私船正以
的速度追截走私船,此时走私船正以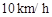 的速度从
的速度从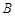 处向北偏东
处向北偏东 方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (
方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (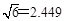 )
)
设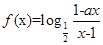 为奇函数,
为奇函数,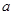 为常数,
为常数,
(1)求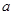 的值;
的值;
(2)证明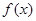 在区间
在区间 上单调递增;
上单调递增;
(3)若 ,不等式
,不等式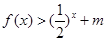 恒成立,求实数
恒成立,求实数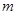 的取值范围。
的取值范围。