(本小题满分12分)已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明: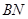 ⊥平面
⊥平面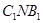 ;
;
(Ⅱ)求平面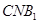 与平面
与平面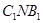 所成角的余弦值;
所成角的余弦值;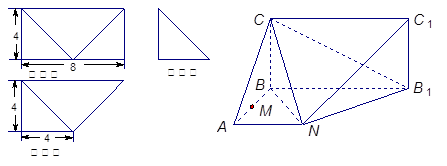
第七届城市运动会2011年10月16日在江西南昌举行,为了搞好接待工作,运动会组委会在某大学招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“ 非高个子”,且只有“女高个子”才担任“礼仪小姐”。(I)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?(II)若从所有“高个子”中选3名志愿者,用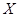 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出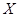 的分布列,并求
的分布列,并求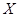 的数学期望。
的数学期望。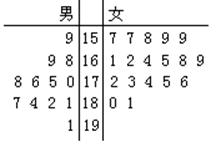
△ABC中,角A、B、C对边分别是a、b、c,满足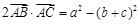 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求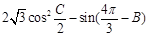 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
)设点C为曲线y=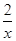 (x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(1)证明:多边形EACB的面积是定值,并求这个定值;
(2)设直线y=-2x+4与圆C交于点M,N,若|EM|=|EN|,求圆C的方程.
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列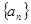 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列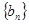 的前六项.(Ⅰ)求等比数列
的前六项.(Ⅰ)求等比数列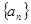 的通项公式;
的通项公式;
(Ⅱ)求等差数列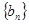 的通项公式;(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
的通项公式;(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率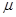 的大小.
的大小.