某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴(即双曲线的虚轴)旋转所成的曲面,其中A、A′是双曲线的顶点,C、C′是冷却塔上口直径的两个端点,B、B′是下底直径的两个端点,已知AA′=14m,CC′=18m,BB′=22m,塔高20m.
|
(Ⅰ)建立坐标系并写出该双曲线方程;
(Ⅱ)求冷却塔的容积(精确到10m3,塔壁厚度不计,π取3.14).(本小题满分14分) 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0).
(1)求f(x)的解析式
(2)定义函数g(x)=f(x)·(x-1),求函数g(x)的最大值。
(本小题满分12分)已知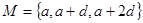 ,
, ,
,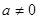 ,M=N,求q的值
,M=N,求q的值
(本小题满分12分)定义A⊗B={z|z=xy+ ,x∈A,y∈B}.设集合A={0,2},B={1,2}
,x∈A,y∈B}.设集合A={0,2},B={1,2}
1.求集合A⊗B的所有元素之和. 2.写出集合A⊗B的所有真子集。
已知函数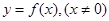 对于任意的
对于任意的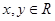 且
且 满足
满足 .
.
(1)求 的值;
的值;
(2)判断函数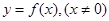 的奇偶性;
的奇偶性;
(3)若函数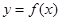 在
在 上是增函数,解不等式
上是增函数,解不等式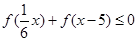 .
.
如图,已知底角为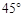 的等腰梯形
的等腰梯形 ,底边
,底边 长为
长为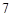 cm,腰长为
cm,腰长为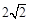 cm,当一条垂直于底边
cm,当一条垂直于底边 (垂足为
(垂足为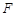 )的直线
)的直线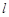 从左至右移动(与梯形
从左至右移动(与梯形 有公共点)时,直线
有公共点)时,直线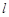 把梯形分成两部分,令
把梯形分成两部分,令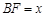 .
.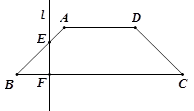
(1)求左边部分的面积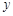 关于
关于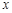 的函数解析式
的函数解析式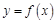 ;
;
(2)作出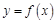 的图象.
的图象.