已知正方体ABCD－A1B1C1D1的棱长为2，点E为棱AB的中点，求：
（Ⅰ）D1E与平面BC1D所成角的大小；
（Ⅱ）二面角D－BC1－C的大小；
（Ⅲ）异面直线B1D1与BC1之间的距离．
如图所示，在四棱锥
中，底面四边形
是菱形，
,
是边长为2的等边三角形，
,
.
（Ⅰ）求证：
底面；
（Ⅱ）求直线
与平面
所成角的大小；
（Ⅲ）在线段
上是否存在一点
，使得
∥平面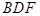
？如果存在，求
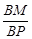的值，如果不存在，请说明理由．
根据以往的成绩记录，甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.
假设每名队员每次射击相互独立.
（Ⅰ）求上图中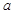
的值；
（Ⅱ）队员甲进行三次射击，求击中目标靶的环数不低于8环的次数
的分布列及数学期望（频率当作概率使用）；
（Ⅲ）由上图判断，在甲、乙两名队员中，哪一名队员的射击成绩更稳定？（结论不需证明）
函数
.
（Ⅰ）在
中，
，求
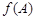的值；
（Ⅱ）求函数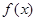
的最小正周期及其图象的所有对称轴的方程.
已知函数
的自变量的取值区间为A，若其值域区间也为A，则称A为的保值区间.
（Ⅰ）求函数
形如
的保值区间；
（Ⅱ）函数
是否存在形如
的保值区间？若存在，求出实数
的值，若不存在，请说明理由.
已知函数
.
（Ⅰ）当
时，求
值；
（Ⅱ）若存在区间
(
且
)，使得
在上至少含有6个零
点，在满足上述条件的中，求
的最小值.