在平面直角坐标系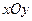
中，有一个以
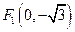和
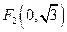为焦点、离心率为
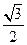的椭圆，设椭圆在第一象限的部分为曲线C，动点P在C上，C在点P处的切线与
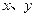轴的交点分别为A、B，且向量
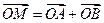。求：
（Ⅰ）点M的轨迹方程； （Ⅱ）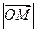
的最小值。
已知f(x)＝logax(a>0且a≠1)，如果对于任意的x∈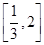
都有|f(x)|≤1成立，试求a的取值范围．
设f(x)＝loga(1＋x)＋loga(3－x)(a>0，a≠1)，且f(1)＝2.
(1)求a的值及f(x)的定义域．
(2)求f(x)在区间
上的最大值．
已知函数f(x)＝3x－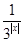
.
(1)若f(x)＝2，求x的值；
(2)判断x>0时，f(x)的单调性；
(3)若3tf(2t)＋mf(t)≥0对于t∈
恒成立，求m的取值范围．
设a>0且a≠1，函数y＝a2x＋2ax－1在[－1,1]上的最大值是14，求a的值．
已知函数f(x)＝ax2－2ax＋2＋b(a≠0)，若f(x)在区间[2,3]上有最大值5，最小值2.
(1)求a，b的值；
(2)若b<1，g(x)＝f(x)－mx在[2,4]上单调，求m的取值范围．