A.选修4-1 几何证明选讲
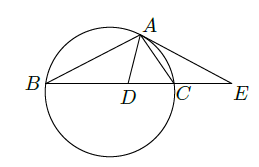
如图,设 的外接圆的切线 与 的延长线交于点 , 的平分线与 交于点 .求证: .
B.选修4-2 矩阵与变换
在平面直角坐标系 中,设椭圆 在矩阵对应的变换作用下得到曲线 ,求 的方程.
C.选修4-4 参数方程与极坐标
在平面直角坐标系 中,点 是椭圆 上的一个动点,求 的最大值.
D.选修4-5 不等式证明选讲
设 为正实数,求证: .
(本小题满分13分)如图,在四棱柱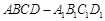 中,底面
中,底面 是矩形,且
是矩形,且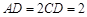 ,
,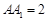 ,
,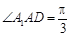 .若
.若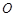 为
为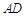 的中点,且
的中点,且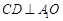 .
.
(1)求证: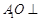 平面
平面 ;
;
(2)线段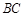 上是否存在一点
上是否存在一点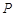 ,使得二面角
,使得二面角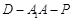 为
为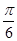 ?若存在,求出
?若存在,求出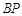 的长;不存在,说明理由.
的长;不存在,说明理由.
(本小题满分13分)某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(1)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(2)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为 ,猜对第3条的概率为
,猜对第3条的概率为 .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
(本小题满分13分)将射线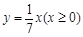 绕着原点逆时针旋转
绕着原点逆时针旋转 后所得的射线经过点
后所得的射线经过点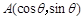 .
.
(1)求点 的坐标;
的坐标;
(2)若向量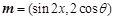 ,
,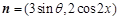 ,求函数
,求函数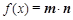 ,
,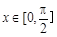 的值域.
的值域.
(本小题满分14分)已知函数 (
( 为常数).
为常数).
(Ⅰ)已知 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求
时,求 的值域;
的值域;
(Ⅲ)设 ,若存在
,若存在 ,
, ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,已知抛物线 :
: 的准线为直线
的准线为直线 ,过点
,过点 的动直线
的动直线 交抛物线
交抛物线 于
于 ,
, 两点.
两点.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)若以线段 为直径的圆恒过抛物线
为直径的圆恒过抛物线 上的某定点
上的某定点 (异于
(异于 两点),求
两点),求 的值和点
的值和点 的坐标.
的坐标.