小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。
凸四边形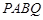 中,其中
中,其中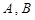 为定点,
为定点,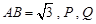 为动点,满足
为动点,满足 .
.
(1)写出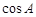 与
与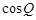 的关系式;
的关系式;
(2)设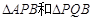 的面积分别为
的面积分别为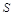 和
和 ,求
,求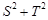 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形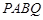 的面积。
的面积。
如图,长方体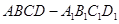 中,
中,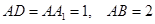 ,点
,点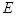 是
是 的中点.
的中点.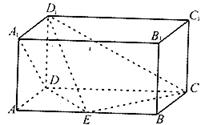
(1)求三棱锥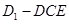 的体积;
的体积;
(2)证明: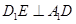 ;
;
(3)求二面角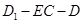 的正切值.
的正切值.
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.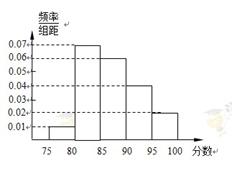
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
② 学校决定在这6名学生中随机抽取2名学生接受考官的面试,设第4组中有X名学生被考官面试,求X的分布列和数学期望.
已知函数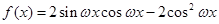 (
(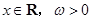 ),其图象相邻两条对称轴之间的距离等于
),其图象相邻两条对称轴之间的距离等于 .
.
(1)求 的值;
的值;
(2)当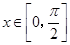 时,求函数
时,求函数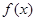 的最大值和最小值及相应的
的最大值和最小值及相应的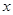 值.
值.