在等差数列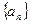 中,
中, ,
,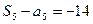 ,其中
,其中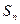 是数列
是数列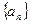 的前
的前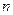 项之和,曲线
项之和,曲线 的方程是
的方程是 ,直线
,直线 的方程是
的方程是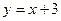 .
.
(1) 求数列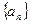 的通项公式;
的通项公式;
(2) 当直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点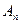 ,
,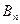 时,令
时,令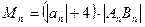 ,
,
求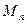 的最小值;
的最小值;
(3) 对于直线 和直线外的一点P,用“
和直线外的一点P,用“ 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线 与直线
与直线 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线 与直线
与直线 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线 的“距离”.
的“距离”.
(本小题满分14分)某商场进行促销活动,到商场购物消费满100元就可转动转盘(转盘为十二等分的圆盘)一次进行抽奖,满200元转两次,以此类推(奖金累加);转盘的指针落在A区域中一等奖,奖10元,落在B、C区域中二等奖,奖5元,落在其它区域则不中奖.一位顾客一次购物消费268元,
(Ⅰ)求该顾客中一等奖的概率;
(Ⅱ)记 为该顾客所得的奖金数,求其分布列;
为该顾客所得的奖金数,求其分布列;
(Ⅲ)求数学期望 (精确到0.01).
(精确到0.01).
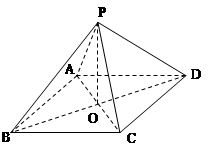
(本小题满分14分)已知四棱锥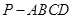 的底面
的底面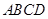 为菱形,且
为菱形,且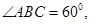
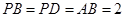 ,
,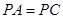 ,
, 与
与 相交于点
相交于点 .
.
(Ⅰ)求证: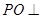 底面
底面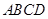 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若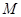 是
是 上的一点,且
上的一点,且 ,求
,求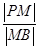 的值.
的值.
(本小题满分13分) 在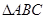 中,角
中,角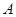 、
、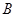 、
、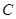 所对的边分别为
所对的边分别为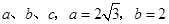 ,
,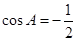 .
.
(Ⅰ)求角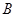 的大小;
的大小;
(Ⅱ)若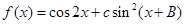 ,求函数
,求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(本小题满分13分)已知集合 ,其中
,其中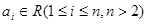 ,
,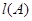 表示和
表示和 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)设集合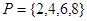 ,
,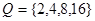 ,分别求
,分别求 和
和 ;
;
(Ⅱ)若集合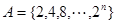 ,求证:
,求证: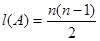 ;
;
(Ⅲ)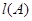 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
(本小题满分14分)已知点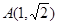 是离心率为
是离心率为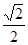 的椭圆
的椭圆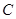 :
: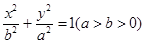 上的一点.斜率为
上的一点.斜率为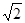 的直线
的直线 交椭圆
交椭圆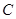 于
于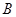 、
、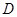 两点,且
两点,且 、
、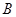 、
、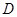 三点不重合.
三点不重合.
(Ⅰ)求椭圆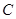 的方程;
的方程;
(Ⅱ)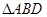 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
(Ⅲ)求证:直线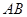 、
、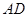 的斜率之和为定值.
的斜率之和为定值.