如图,某住宅小区的平面图呈圆心角为 的扇形 ,小区的两个出入口设置在点 及点 处,且小区里有一条平行于 的小路 ,已知某人从 沿 走到 用了10分钟,从 沿 走到 用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径 的长(精确到1米).

本题共有2个小题,第1小题满分6分,第2小题满分8分.
在二项式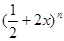 的展开式中:
的展开式中:
(1)若第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;
(2)若所有项的二项式系数和等于4096,求展开式中系数最大的项.
如图,直线 平面
平面 ,
, 为正方形,
为正方形, ,求直线
,求直线 与
与 所成角的大小.
所成角的大小.
已知函数 ,函数
,函数 .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若对任意 ,均存在
,均存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆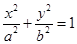 的左焦点
的左焦点 为圆
为圆 的圆心,且椭圆上的点到点
的圆心,且椭圆上的点到点 的距离的最小值为
的距离的最小值为 .
.
(1)求椭圆的方程;
(2)已知经过点 的动直线
的动直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,点
,点 ,求
,求 的值.
的值.
已知圆 过
过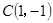 ,
, 两点,且圆心
两点,且圆心 在
在 上.
上.
(1)求圆 的方程;
的方程;
(2)设点 是直线
是直线 上的动点,
上的动点,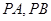 是圆
是圆 的两条切线,
的两条切线, 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.