已知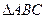 中,
中, ,
, ,
, ,记
,记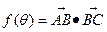 ,
,
(1)求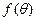 关于
关于 的表达式;
的表达式;
(2)求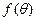 的值域;
的值域;
(本小题满分12分) 在 中,内角
中,内角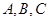 所对边的长分别为
所对边的长分别为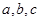 ,已知向量
,已知向量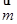 ="(1,cosA" -1),
="(1,cosA" -1), =(cosA,1)且满足
=(cosA,1)且满足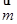 ⊥
⊥ .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
(本小题满分14分)
已知 ,函数
,函数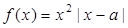 .
.
(Ⅰ)当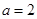 时,求使
时,求使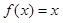 成立的
成立的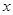 的集合;
的集合;
(Ⅱ)求函数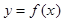 在区间
在区间 上的最小值.
上的最小值.
(本小题满分14分)
已知抛物线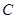 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在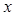 轴上. 且经过点
轴上. 且经过点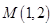 ,
,
(1)求抛物线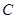 的方程;
的方程;
(2)若动直线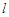 过点
过点 ,交抛物线
,交抛物线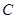 于
于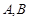 两点,是否存在垂直于
两点,是否存在垂直于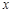 轴的直线
轴的直线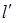 被以
被以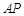 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出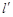 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分14分)
已知曲线 :
: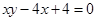 ,数列
,数列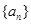 的首项
的首项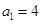 ,且当
,且当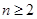 时,点
时,点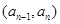 恒在曲线
恒在曲线 上,数列
上,数列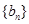 满足
满足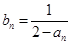 。
。
(1)试判断数列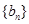 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列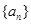 和
和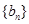 的通项公式;
的通项公式;
(3)设数列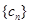 满足
满足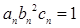 ,试比较数列
,试比较数列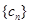 的前
的前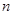 项和
项和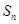 与2的大小。
与2的大小。
(本小题满分14分)
如图,沿等腰直角三角形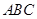 的中位线
的中位线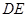 ,将平面
,将平面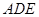 折起,平面
折起,平面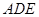 ⊥平面
⊥平面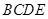 ,得到四棱锥
,得到四棱锥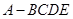 ,
,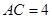 ,设
,设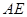 、
、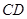 的中点分别为
的中点分别为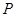 、
、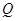 ,
,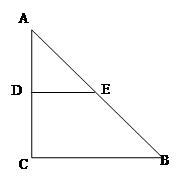
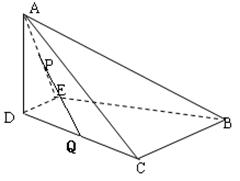
(1)求证:平面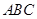 ⊥平面
⊥平面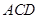
(2)求证:
(3)求平面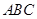 与平面
与平面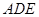 所成锐二面角的余弦值。
所成锐二面角的余弦值。