如图,在四棱锥
中,底面
是矩形.已知
.
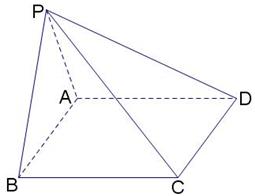
(Ⅰ)证明
平面
;
(Ⅱ)求异面直线
与
所成的角的大小;
(Ⅲ)求二面角
的大小.
(理)数列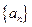 的前
的前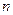 项和记为
项和记为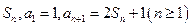
(Ⅰ)求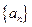 的通项公式;
的通项公式;
(Ⅱ)等差数列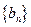 的各项为正,其前
的各项为正,其前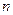 项和为
项和为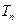 ,且
,且 ,又
,又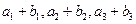 成等比数列,求
成等比数列,求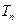
(本小题满分12分)(文)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)(文)求甲获得这次比赛胜利的概率。
(理)设进入某商场的每一位顾客购买甲种商品的概率为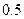 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记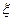 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求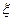 的分布列及期望。
的分布列及期望。
(文)已知向量m=(sinA,cosA),n=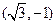 ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;(Ⅱ)求函数 的值域.
的值域.
(理)已知向量m=(sinA,cosA),n= ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;(Ⅱ)求函数 的值域.
的值域.