(本小题满分13分)已知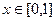 ,函数
,函数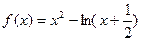 ,
,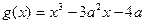 .
.
(Ⅰ)求函数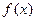 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设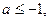 若
若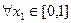 ,总存在
,总存在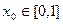 ,使得
,使得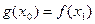 成立,求
成立,求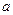 的取值范围.
的取值范围.
(本小题满分16分)
已知函数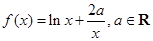 .
.
(1)若x=2是函数f(x)的极值点,求实数a的值.
(2)若函数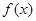 在
在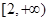 上是增函数,求实数
上是增函数,求实数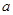 的取值范围;
的取值范围;
(3)若函数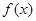 在
在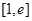 上的最小值为3,求实数
上的最小值为3,求实数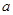 的值.
的值.
(本小题满分16分)
已知圆C过点P(1,1),且与圆M: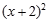 +
+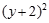 =
=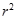 (r>0)关于直线x+y+2=0对称.
(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)直线l过点Q(1,0.5),截圆C所得的弦长为2,求直线l的方程;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
(本小题满分14分)
某市郊区一村民小组有100户农民,且都从事蔬菜种植.据调查,平均每户的年收入为3万元.为了调整产业结构,郊区政府决定动员该村部分农民从事蔬菜加工.据预测,若能动员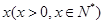 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高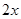 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为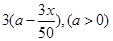 万元.
万元.
(1)在动员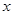 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求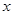 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求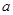 的最大值.
的最大值.
(本小题满分14分)
已知数列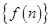 的前n项和为
的前n项和为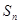 ,且
,且 .
.
(Ⅰ)求数列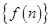 通项公式;
通项公式;
(Ⅱ)若 ,
, ,求证数列
,求证数列 是等比数列,并求数
是等比数列,并求数
列 的前
的前 项和
项和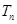 .
.
(本小题满分14分)
已知函数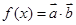 ,其中
,其中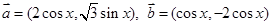
(1)求函数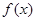 在区间
在区间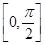 上的值域;
上的值域;
(2)在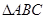 中,
中,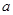 .
.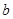 ,
,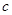 分别是角
分别是角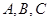 的对边,
的对边,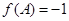 ,且
,且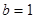
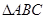 的面积
的面积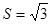 ,求边
,求边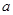 的值.
的值.