2010年5月1日,上海世博会将举行,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。求A能够入选的概率;
规定:按人选人数得训练经费(每人选1人,则相应的训练基地得到3000元的训练经费),求该基地得到训练经费的分布列与数学期望。
设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1, )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线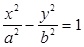 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
已知抛物线、椭圆和双曲线都经过点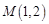 ,它们在
,它们在 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求这三条曲线的方程;
(2)已知动直线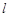 过点
过点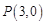 ,交抛物线于
,交抛物线于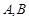 两点,是否存在垂直于
两点,是否存在垂直于 轴的直线
轴的直线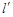 被以
被以 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出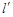 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知抛物线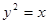 的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
的弦AB与直线y=1有公共点,且弦AB的中点N到y轴的距离为1,求弦AB长度的最大值,并求此直线AB所在的直线的方程.
已知双曲线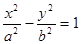 的离心率
的离心率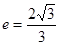 ,过
,过 的直线到原点的距离是
的直线到原点的距离是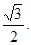
(1)求双曲线的方程;
(2)已知直线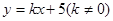 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
已知抛物线y2=8x上两个动点A、B及一个定点M(x0, y0),F是抛物线的焦点,且|AF|、|MF|、|BF|成等差数列,线段AB的垂直平分线与x轴交于一点N.
(1)求点N的坐标(用x0表示);
(2)过点N与MN垂直的直线交抛物线于P、Q两点,若|MN|=4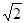 ,求△MPQ的面积.
,求△MPQ的面积.