已知抛物线y2=8x上两个动点A、B及一个定点M（x0, y0），F是抛物线的焦点，且|AF|、|MF|、|BF|成等差数列，线段AB的垂直平分线与x轴交于一点N．
（1）求点N的坐标（用x0表示）；
（2）过点N与MN垂直的直线交抛物线于P、Q两点，若|MN|=4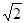
，求△MPQ的面积．
如图，已知三棱柱ABC－A1B1C1中，侧棱A A1⊥底面ABC
AB⊥BC；
（Ⅰ）求证：平面A1BC⊥侧面A1ABB1.
（Ⅱ）若
,直线AC与平面A1BC所成的角为
，
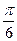求AB的长。
过点Q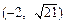 
作圆C：x2＋y2＝r2(
)的切线，切点为D，且QD＝4．
(1)求r的值；
(2)设P是圆C上位于第一象限内的任意一点，过点P作圆C的切线l，且l交x轴于点A，交y 轴于点B，设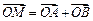
，求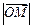
的最小值(O为坐标原点).
如图，已知三棱柱ABC－A1B1C1中，侧棱A A1⊥底面ABC
AB⊥BC；
（Ⅰ）求证：平面A1BC⊥侧面A1ABB1.
（Ⅱ）若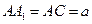
,直线AC与平面A1BC所成的角为
，
求AB的长。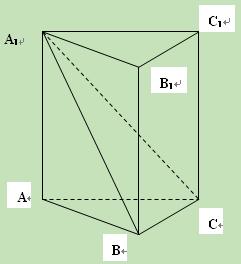
已知数列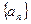
的首项为
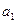=3，通项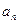
与前n项和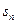
之间满足2=·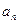
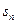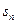
（n≥2）。
(1)求证：
是等差数列，并求公差；
(2)求数列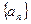的通项公式。
设△ABC的内角A，B，C的对边分别为a,b,c.已知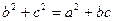
，求：
（Ⅰ）A的大小;
（Ⅱ）若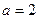
，求
面积的最大值.