如图,已知直三棱柱ABC—A1B1C1,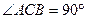 ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,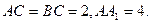
(1)求证: ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。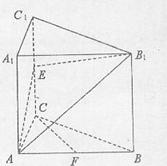
(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: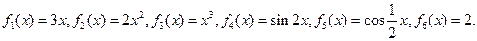
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是偶函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数的卡片则停止抽取,否则继续进行. 求抽取次数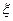 的分布列、数学期望和方差.
的分布列、数学期望和方差.
(本小题满分12分)
已知函数 R).(1)若
R).(1)若 在
在 时取得极值,求
时取得极值,求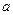 的值;
的值;
(2)求 的单调区间;(3)求证:当
的单调区间;(3)求证:当 时,
时, .
.
(本小题满分12分)
如图:在三棱锥 中,
中,
 是直角三角形,
是直角三角形,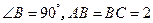 ,
, ,点
,点 、
、 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证: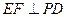 ;
;
(Ⅱ)求直线 与平面
与平面 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角 的正切值.
的正切值.
(本小题满分12分)
在数列 中,已知
中,已知 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 且
且 的前项
的前项 和为
和为 ,求证:
,求证: .
.
(本小题满分12分)
已知向量 ,
,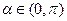 ,
, ,向量
,向量 与
与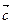 的夹角为
的夹角为 ,向量
,向量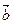 与
与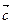 的夹角为
的夹角为 ,且
,且 .若
.若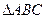 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为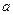 、
、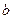 、
、 ,且角
,且角 .
.
(1)求角 的大小;
的大小;
(2)若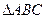 的外接圆半径为
的外接圆半径为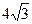 ,试求
,试求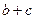 的取值范围.
的取值范围.