如图，在底面是正方形的四棱锥P—ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一点.
（I）求证：BD⊥FG；
（II）确定点G在线段AC上的位置，使FG//平面PBD，并说明理由.
（III）当二面角B—PC—D的大小为
时，求PC与底面ABCD所成角的正切值.
已知a，b为正实数．
(1)求证：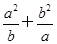
≥a＋b；
(2)利用(1)的结论求函数y＝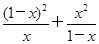
(0<x<1)的最小值．
已知函数f(x)＝|x＋3|＋|x－a|(a>0)．
(1)当a＝4时，已知f(x)＝7，求x的取值范围；
(2)若f(x)≥6的解集为{x|x≤－4或x≥2}，求a的值．
设函数f(x)＝|x－1|＋|x－2|.
(1)画出函数y＝f(x)的图象；
(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．
设不等式|x－2|<a(a∈N*)的解集为A，且
∈A，
∉A.
(1)求a的值；
(2)求函数f(x)＝|x＋a|＋|x－2|的最小值．
已知a≥b>0，求证：2a3－b3≥2ab2－a2b.