心脏每跳动一次,就完成一次收缩和舒张.心脏跳动时,血压在增大或减小,并呈周期性变化.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压.健康成年人的收缩压和舒张压一般为120~140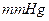 和60~90
和60~90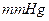 . 设某成年人的血压满足函数式
. 设某成年人的血压满足函数式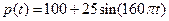 ,其中
,其中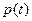 为血压
为血压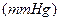 ,
,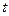 为时间
为时间 ,
, .试回答下列问题:
.试回答下列问题:
(Ⅰ)求函数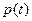 的周期;
的周期;
(Ⅱ)求此人每分钟心跳的次数;
(Ⅲ)求出此人的血压在血压计上的读数,并说明此人的血压是否正常.
(Ⅳ)在某些时间段内,此人的血压是持续升高的.试写出所有这样的时间段.