(本小题满分12分)
在四棱锥 中,底面
中,底面 是一直角梯形,
是一直角梯形,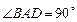 ,
, ,
,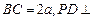 底面
底面 .
.
(1)在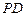 上是否存在一点
上是否存在一点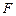 ,使得
,使得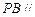 平面
平面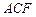 ,若存在,求出
,若存在,求出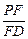 的值;
的值;
若不存在,试说明理由;
(2)在(1)的条件下,若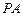 与
与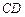 所成的角为
所成的角为 ,求二面角
,求二面角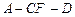 的余弦值.
的余弦值.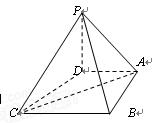
几何证明选讲 如图,已知 、
、 是圆
是圆 的两条弦,且
的两条弦,且 是线段
是线段 的垂直平分线,已知
的垂直平分线,已知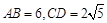 ,求线段
,求线段 的长度.
的长度.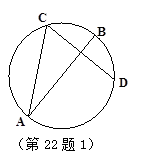
(本小题满分12分)三次函数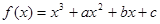 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求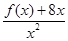 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求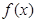 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为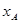 ,
,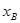 ,
,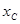 ,
,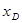 求证
求证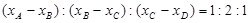 ;
;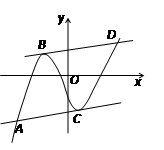
(本小题满分12分)设椭圆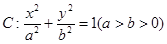 的左、右焦点分别为
的左、右焦点分别为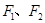 ,上顶点为
,上顶点为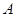 ,在
,在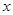 轴负半轴上有一点
轴负半轴上有一点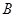 ,满足
,满足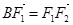 ,且
,且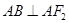 .
.
(1)求椭圆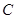 的离心率;
的离心率;
(2)若过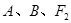 三点的圆恰好与直线
三点的圆恰好与直线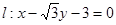 相切,求椭圆
相切,求椭圆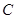 的方程;
的方程;
(3)在(2)的条件下,过右焦点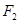 作斜率为
作斜率为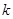 的直线
的直线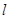 与椭圆
与椭圆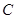 交于
交于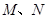 两点,在
两点,在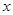 轴上是否存在点
轴上是否存在点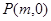 ,使得以
,使得以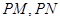 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出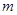 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。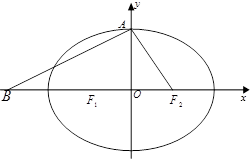
(本小题满分12分)如图,在多面体 中,
中,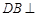 平面
平面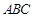 ,
,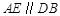 ,且
,且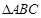 是边长为2的等边三角形,
是边长为2的等边三角形,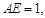
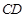 与平面
与平面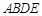 所成角的正弦值为
所成角的正弦值为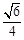 .
.
(Ⅰ)在线段 上存在一点F,使得
上存在一点F,使得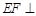 面
面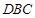 ,试确定F的位置;
,试确定F的位置;
(Ⅱ)求二面角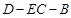 的平面角的余弦值.
的平面角的余弦值.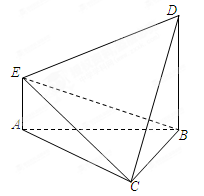
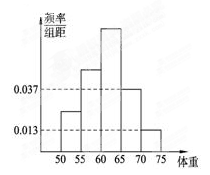
(本小题满分12分)为了解今年某校高三毕业班准备报考飞行员学生的体重情
况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前 个小组的频率之比为
个小组的频率之比为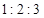 ,其中第
,其中第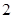 小组的频数为
小组的频数为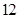 .
.
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.