(本小题满分12分)
已知椭圆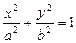 (
(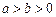 )的离心率为
)的离心率为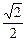 ,且短轴长为2.
,且短轴长为2.
(1)求椭圆的方程;
(2)若与两坐标轴都不垂直的直线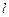 与椭圆交于
与椭圆交于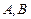 两点,
两点,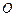 为坐标原点,且
为坐标原点,且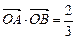 ,
,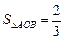 ,求直线
,求直线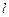 的方程.
的方程.
已知函数 .
.
(I)求函数 的最小值;
的最小值;
(II)若 ,求
,求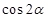 的值.
的值.
已知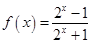 .
.
(I)判断 的奇偶性;
的奇偶性;
(II)求 的值域.
的值域.
数学运算中,常用符号来表示算式,如 =
= ,其中
,其中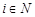 ,
, .
.
(Ⅰ)若 ,
,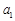 ,
,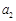 ,…,
,…, 成等差数列,且
成等差数列,且 ,公差
,公差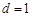 ,求证:
,求证:
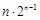 ;
;
(Ⅱ)若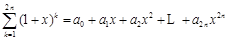 ,
, ,记
,记 ,且不等式
,且不等式 对于
对于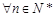 恒成立,求实数
恒成立,求实数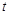 的取值范围.
的取值范围.
抛掷甲,乙两枚质地均匀且四面上分别标有1,2,3,4的正四面体,其底面落于桌面,记底面上所得的数字分别为x,y.记 表示
表示 的整数部分,如:
的整数部分,如: ,设
,设 为随机变量,
为随机变量,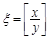 .
.
(Ⅰ)求概率 ;
;
(Ⅱ)求 的分布列,并求其数学期望
的分布列,并求其数学期望 .
.
在极坐标系中,直线 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为
,以极点为原点,极轴为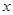 轴的正半轴建立平面直角坐标系,曲线
轴的正半轴建立平面直角坐标系,曲线 的参数方程为
的参数方程为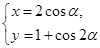 (
(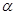 为参数),求直线
为参数),求直线 与曲线
与曲线 的交点P的直角坐标.
的交点P的直角坐标.