(本小题满分10分)
选修4-4:坐标系与参数方程选讲
已知曲线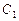 的参数方程为
的参数方程为 (
(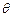 为参数),曲线
为参数),曲线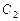 的参数方程为
的参数方程为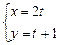 (
(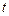 为参数).
为参数).
(1)若将曲线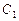 与
与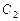 上各点的横坐标都缩短为原来的一半,分别得到曲线
上各点的横坐标都缩短为原来的一半,分别得到曲线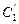 和
和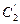 ,求出曲线
,求出曲线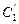 和
和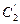 的普通方程;
的普通方程;
(2)以坐标原点为极点,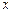 轴的非负半轴为极轴建立极坐标系,求过极点且与
轴的非负半轴为极轴建立极坐标系,求过极点且与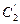 垂直
垂直 的直线的极坐标方程.
的直线的极坐标方程.
已知:集合 ,集合
,集合 ,
,
求 .
.
已知函数 .
.
(1)试判断函数F(x)=(x2+1) f (x) – g(x)在[1,+∞)上的单调性;
(2)当0<a<b时,求证:函数f (x) 定义在区间[a,b]上的值域的长度大于 (闭区间[m,n]的长度定义为n –m).
(闭区间[m,n]的长度定义为n –m).
(3)方程f(x)= 是否存在实数根?说明理由。
是否存在实数根?说明理由。
已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.
向量 满足
满足 ∥
∥ .(1)求sinA+sinB的取值范围;
.(1)求sinA+sinB的取值范围;
(2)若 ,且实数x满足
,且实数x满足 ,试确定x的取值范围.
,试确定x的取值范围.
已知二次函数
 ,若不等式
,若不等式
 的解集为
的解集为 .
.
(1)求集合 ;
;
(2)若方程
 在C上有解,求实数
在C上有解,求实数 的取值范围.
的取值范围.
已知函数 满足
满足 且对于任意
且对于任意 , 恒有
, 恒有 成立. (1)求实
成立. (1)求实 数
数 的值; (2)解不等式
的值; (2)解不等式 .
.