中,角所对的边分别为.已知 求 和的值.
在极坐标系中,已知点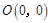 ,
,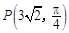 ,求以
,求以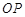 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
设矩阵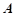
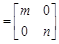 ,若矩阵
,若矩阵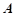 的属于特征值1的一个特征向量为
的属于特征值1的一个特征向量为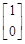 ,属于特征值2的一个特征向量为
,属于特征值2的一个特征向量为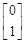 ,求实数
,求实数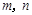 的值.
的值.
(本小题满分16分)已知函数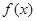 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: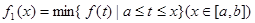 ,
,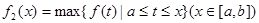
其中,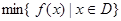 表示函数
表示函数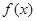 在区间上的最小值,
在区间上的最小值,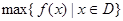 表示函数
表示函数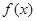 在区间上的最大值.若存在最小正整数
在区间上的最大值.若存在最小正整数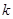 ,使得
,使得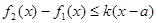 对任意的
对任意的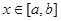 成立,则称函数为区间
成立,则称函数为区间 上的“
上的“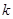 阶收缩函数”.
阶收缩函数”.
(1)若 ,试写出
,试写出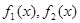 的表达式;
的表达式;
(2)已知函数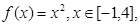 试判断
试判断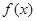 是否为
是否为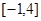 上的“
上的“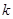 阶收缩函数”,如果是,求出相应的
阶收缩函数”,如果是,求出相应的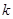 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知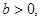 函数
函数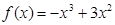 是
是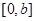 上的2阶收缩函数,求
上的2阶收缩函数,求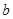 的取值范围.
的取值范围.
(本小题满分16分)记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+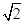 ,S3=12+
,S3=12+ .
.
(1)求数列{an}的通项公式an及前n项和Sn;
(2)记bn=an-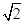 ,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且
,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且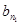 ,
,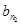 ,…,
,…, ,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
(3)试问:在数列{an}中是否存在三项ar,as,at(r<s<t,r,s,t∈N*)恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
(本小题满分15分)已知椭圆C: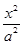 +
+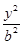 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且经过点P(1,
,且经过点P(1, ).
).
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M.问点M满足什么条件时,圆M与y轴有两个交点? 并求两点间距离的最大值.