某教师出了一份共3道题的测试卷,每道题1分。全班的3分、2分、1分和0分的学生所占的比例分别为30%,50%,10%和10%。
(1)若全班共10人,则平均分是多少?
(2)若全班共20人,则平均分是多少?
(3)若该班人数未知,能求出该班的平均分吗?
已知函数 .
.
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)函数 在区间[1,2]上是否有零点,若有,求出零点,若没有,请说明理由;
在区间[1,2]上是否有零点,若有,求出零点,若没有,请说明理由;
(Ⅲ)若任意的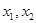 ∈(1,2)且
∈(1,2)且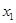 ≠
≠ ,证明:
,证明: (注:
(注: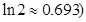
(本小题满分12分)已知焦点在 轴上的椭圆C1:
轴上的椭圆C1: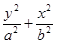 =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为 .
.
(I)求椭圆C1的方程;
(Ⅱ)过抛物线C2: (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与 轴平行时,求h的最小值.
轴平行时,求h的最小值.
(本小题满分12分)如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AB,M、N分别是PA、BC的中点.
(I)求证:MN∥平面PCD;
(II)在棱PC上是否存在点E,使得AE上平面PBD?若存在,求出AE与平面PBC所成角的正弦值,若不存在,请说明理由
(本小题满分12分)某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
(I)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
(II)从专业A中随机抽取2名学生,记其中女生的人数为X,求X的分布列和均值.
注:

(本小题满分12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.