(本小题满分12分)某城市有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC、△ABD，经测量AD=BD=14，BC=10,AC=16,∠C=∠D．
(I)求AB的长度；
(Ⅱ)若建造环境标志的费用与用地面积成正比，不考虑其他因素，小李、小王谁的设计使建造费用最低，请说明理由．
已知函数
的图像过点
，且b>0，又
的最大值为
.
（Ⅰ）将写成含
的形式；
（Ⅱ）由函数y =图像经过平移是否能得到一个奇函数y =
的图像？若能，请写出平移的过程；若不能，请说明理由。
函数f(x)=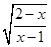
的定义域为集合A，关于x的不等式22ax<2a+x(a∈R)的解集为B，求使A∩B=A的实数a的取值范围．
已知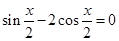
．
（I）求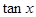
的值；
（Ⅱ）求
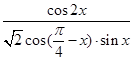的值．
已知函数f (x)＝x＋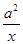
，g(x)＝x＋ln x，其中a＞0.
(1) 若x＝1是函数h (x)＝f (x)＋g (x)的极值点，求实数a的值；
(2)若对任意的x1，x2∈[1，e](e为自然对数的底数)都有f(x1)≥g(x2)成立，
求实数a的取值范围．
已知数列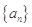
的前
项和
与
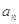满足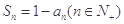
.
（1）求数列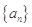的通项公式；（2）求数列
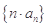的前项和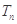
.