设二次方程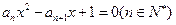 有两个实根
有两个实根 和
和 ,
,
且满足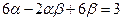 .
.
(1)试用 表示
表示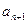 ;
;
(2)求证: 是等比数列;
是等比数列;
(3)当 时,求数列
时,求数列 的通项公式.
的通项公式.
已知P(x,y)是圆x2+y2=2y上的动点.
(1)求2x+y的取值范围;
(2)若x+y+c>0恒成立,求实数c的取值范围
已知直线l的极坐标方程为:ρcos=6,圆O的参数方程为:求直线l与圆O相交所得弦的弦长.
已知直线l的极坐标方程为ρsin=,求点A到直线l的距离.
(本小题满分14分)已知函数 处取得极值.
处取得极值.
(1)求实数a的值,并判断 上的单调性;
上的单调性;
(2)若数列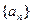 满足
满足 ;
;
(3)在(2)的条件下,记

求证:
在平面直角坐标系xOy中,已知点A(-1, 0)、B(1, 0), 动点C满足条件:△ABC的周长为 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W.
(Ⅰ)求W的方程;
(Ⅱ)经过点(0, 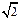 )且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
)且斜率为k的直线l与曲线W有两个不同的交点P和Q,求k的取值范围;
(Ⅲ)已知点M( ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量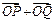 与
与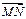 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.