已知等比数列{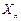 }的各项为不等于1的正数,数列{
}的各项为不等于1的正数,数列{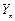 }的通项公式为
}的通项公式为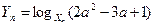 ,其中1<a<
,其中1<a<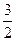 为常数,对于k 、t∈N,k≠t ,满足
为常数,对于k 、t∈N,k≠t ,满足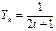 ,
,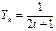 ,
,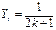 ,是否存在自然数
,是否存在自然数 使得n>
使得n> 时,
时,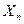 >1恒成立?若存在求出相应的
>1恒成立?若存在求出相应的 ,若不存在,请说明理由。
,若不存在,请说明理由。
在等比数列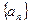 中,
中,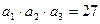 ,
,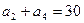
试求:(I)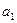 和公比
和公比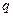 ;(II)前6项的和
;(II)前6项的和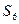 .
.
已知数列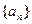 满足
满足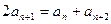
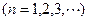 ,它的前
,它的前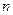 项和为
项和为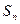 ,且
,且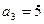 ,
,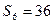 .(1)求
.(1)求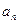 ;(2)已知等比数列
;(2)已知等比数列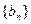 满足
满足 ,
,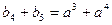
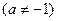 ,设数列
,设数列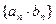 的前
的前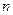 项和为
项和为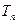 ,求
,求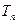 .
.
已知函数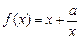 的定义域为
的定义域为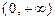 ,且
,且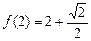 . 设点
. 设点 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点 分别作直线
分别作直线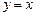 和
和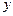 轴的垂线,垂足分别为
轴的垂线,垂足分别为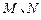 .
.
(1)求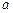 的值;
的值;
(2)问: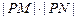 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设 为坐标原点,求四边形
为坐标原点,求四边形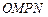 面积的最小值.
面积的最小值.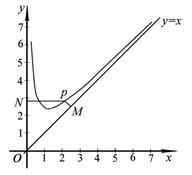
如图,某隧道设计为双向四车道,车道总宽22m,要求通行车辆限高4.5m,隧道全长2.5km,隧道的拱线近似地看成半个椭圆形状。
(1)若最大拱高h为6m,则拱宽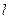 应设计为多少?
应设计为多少?
(2)若最大拱高h不小于6m,则应如何设计拱高h和拱宽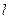 ,才能使建造这个隧道的土方工程量最小(半椭圆面积公式为
,才能使建造这个隧道的土方工程量最小(半椭圆面积公式为 h)?
h)?
某地区发生流行性病毒感染,居住在该地区的居民必须服用一种药物预防,规定每人每天早晚八时各服一片,现知该药片每片含药量为220毫克,若人的肾脏每12小时从体内滤出这种药的60%,在体内的残留量超过386毫克,就将产生副作用.
(1)某人上午八时第一次服药,问到第二天上午八时服完药时,这种药在他体内还残留多少?(2) 长期服用的人这种药会不会产生副作用?