若a、b、c均为正数,求证: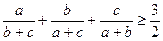 。
。
某人为了获得国外某大学的留学资格,必须依次通过科目一、科目二、科目三3次考试,若某科目考试没通过,则不能参加后面科目的考试,已知他通过科目一、科目二、科目三考试的概率分别为0.9、0.7、0.6.(Ⅰ)求此人顺利获得留学资格的概率;(Ⅱ)设此人在此次申请留学资格的过程中,参加的考试次数为随机变量 ,求
,求 的数学期望.
的数学期望.
已知a、b、c是△ABC三边长,关于x的方程
 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积 (I)求
(I)求 C;(II)求a、b的值.
C;(II)求a、b的值.
22.(本小题满分12分)
A、B是双曲线 ―y2=1上两点,M为该双曲线右准线上一点,且
―y2=1上两点,M为该双曲线右准线上一点,且 =
= .
.
(Ⅰ)求| |的取值范围(O为坐标原点);
|的取值范围(O为坐标原点);
(Ⅱ)是否存在定点N,使| |=|
|=| |总成立?并说明理由.
|总成立?并说明理由.
21.(本小题满分12分)
已知函数f(x)= 在x=1处取得极值(a>0)
在x=1处取得极值(a>0)
(I)求a、b所满足的条件;
(II)讨论函数f(x)的单调性.
20.(本小题满分12分)
已知数列{an}的前n项和Sn=3―an― ,
, .
.
(I)求证: 是等差数列;
是等差数列;
(II)求an的最大值.