如图,三角形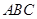 是边长为4的正三角形,
是边长为4的正三角形,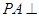 底面
底面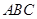 ,
, ,点
,点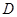 是
是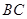 的中点,点
的中点,点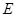 在
在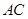 上,且
上,且 .
.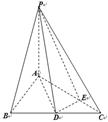
(1)证明:平面 平面
平面 ;
;
(2)求直线 和平面
和平面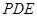 所成角的正弦值.
所成角的正弦值.
如图,在边长为1的正方体ABCD-A1B1C1D1中,求证:
(1)A1C^平面BDC1;
(2)求三棱锥A1—BDC1的体积。
长方体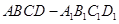 中,
中, ,
, ,点
,点 为
为 中点.
中点.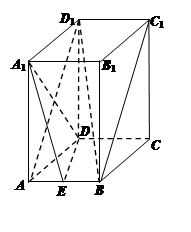
(Ⅰ)求证:
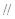 平面
平面 ;
;
(Ⅱ)求证: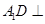 平面
平面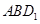 ;
;
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线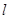 :
: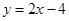 .设圆
.设圆 的半径为1,圆心在
的半径为1,圆心在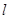 上.
上.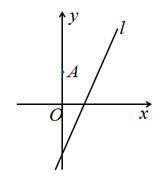
(1)若圆心 也在直线
也在直线 上,过点
上,过点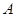 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点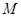 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标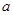 的取值范围.
的取值范围.
如图甲,⊙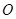 的直径
的直径 ,圆上两点
,圆上两点 在直径
在直径 的两侧,使
的两侧,使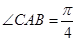 ,
, .沿直径
.沿直径 折起,使两个半圆所在的平面互相垂直(如图乙),
折起,使两个半圆所在的平面互相垂直(如图乙),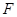 为
为 的中点,
的中点, 为
为 的中点.
的中点. 为
为 上的动点,根据图乙解答下列各题:
上的动点,根据图乙解答下列各题:
(1)求点 到平面
到平面 的距离;
的距离;
(2)求证:不论点 在何位置,都有
在何位置,都有 ⊥
⊥ ;
;
(3)在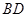 弧上是否存在一点
弧上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.