如图甲,⊙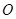 的直径
的直径 ,圆上两点
,圆上两点 在直径
在直径 的两侧,使
的两侧,使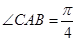 ,
, .沿直径
.沿直径 折起,使两个半圆所在的平面互相垂直(如图乙),
折起,使两个半圆所在的平面互相垂直(如图乙),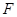 为
为 的中点,
的中点, 为
为 的中点.
的中点. 为
为 上的动点,根据图乙解答下列各题:
上的动点,根据图乙解答下列各题:
(1)求点 到平面
到平面 的距离;
的距离;
(2)求证:不论点 在何位置,都有
在何位置,都有 ⊥
⊥ ;
;
(3)在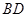 弧上是否存在一点
弧上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本小题满分10分)(选修4—5,:不等式选讲)
(Ⅰ)证明柯西不等式: ;
;
(Ⅱ)若 且
且 ,用柯西不等式求
,用柯西不等式求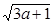 +
+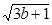 的最大值.
的最大值.
(本小题满分10分)选修4-4:坐标系与参数方程
将圆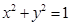 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与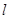 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(本小题满分10分)选修4-1:几何证明选讲.
如图,在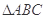 中,
中,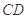 是
是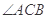 的角平分线,
的角平分线, 的外接圆交
的外接圆交 于点
于点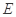 ,
,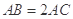 .
.
(Ⅰ)求证: ;
;
(Ⅱ)当 时,求
时,求 的长.
的长.
(本小题满分12分)已知函数f(x)=alnx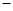 ax
ax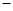 3(a∈R)。
3(a∈R)。
(Ⅰ)求f(x)的单调区间
(Ⅱ)设a=-1,求证:当x∈(1,+∞)时,f(x)+2>0
(Ⅲ)求证: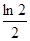 ·
· ·
· ……
……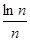 <
< (n∈N+且n≥2)
(n∈N+且n≥2)
(本小题满分12分)设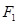 ,
, 分别是椭圆
分别是椭圆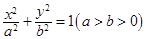 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且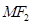 与x轴垂直,直线
与x轴垂直,直线 与C的另一个交点为N.
与C的另一个交点为N.
(Ⅰ)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(Ⅱ)若直线MN在y轴上的截距为2,且 ,求a,b.
,求a,b.