在如图所示的几何体中,四边形 为平行四边形,
为平行四边形, ,
, 平面
平面 ,
, ,
,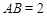 ,
, ,
, ,且
,且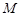 是
是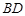 的中点.
的中点.
(Ⅰ)求证: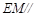 平面
平面 ;
;
(Ⅱ)求二面角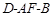 的大小;
的大小;
(Ⅲ)在线段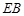 上是否存在一点
上是否存在一点 ,使得
,使得 与
与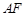 所成的角为
所成的角为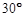 ? 若存在,求出
? 若存在,求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(本题12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面 (编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用
(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用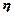 表示更换的面数,用
表示更换的面数,用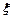 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出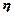 的分布列,求
的分布列,求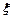 的数学期望。
的数学期望。
.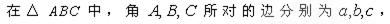
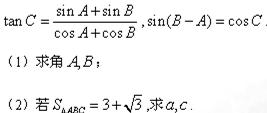
已知数列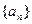 ,
,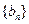 满足
满足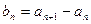 ,其中
,其中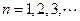 .
.
(1)若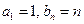 ,求数列
,求数列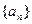 的通项公式;
的通项公式;
(2)若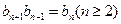 ,且
,且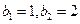 .记
.记 ,
,
求证:数列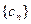 为等差数列;
为等差数列;
设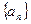 为递增等差数列,Sn为其前n项和,满足
为递增等差数列,Sn为其前n项和,满足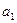
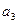 -
-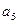 =S10,S11=33。
=S10,S11=33。
(1)求数列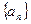 的通项公式
的通项公式 及前n项和Sn;
及前n项和Sn;
(2)试求所有的正整数m,使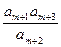 为正整数。
为正整数。
姜堰人民商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
| 资金 |
每台空调或冰箱所需资金(百元) |
月资金供应数量 (百元) |
|
| 空调 |
冰箱 |
||
| 成本 |
30 |
20 |
300 |
| 工人工资 |
5 |
10 |
110 |
| 每台利润 |
6 |
8 |
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?