(本小题满分14分)
在四棱锥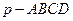 中,侧面
中,侧面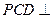 底面
底面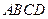 ,
,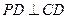 ,
,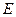 为
为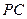 中点,底面
中点,底面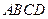 是直角梯形,
是直角梯形,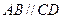 ,
,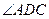 =90°,
=90°,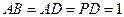 ,
,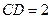 。
。
(I)求证: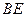
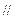 平面
平面 ;
;
(II)求证: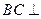 平面
平面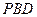 ;
;
(III)设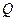 为侧棱
为侧棱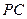 上一点,
上一点, ,试确定
,试确定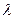 的值,使得二面角
的值,使得二面角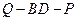 为45°。
为45°。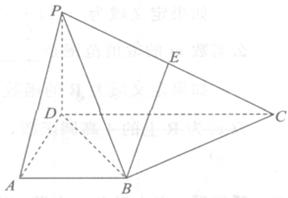
已知椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,点M在椭圆上且位于第一象限,直线FM被圆
,点M在椭圆上且位于第一象限,直线FM被圆 截得的线段的长为c,
截得的线段的长为c,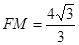 .
.
(Ⅰ)求直线FM的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设椭圆上动点P在x轴上方,若直线FP的斜率大于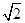 ,求直线OP(O为原点)的斜率的取值范围.
,求直线OP(O为原点)的斜率的取值范围.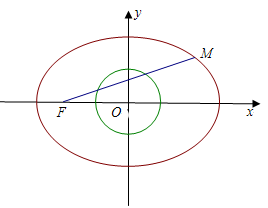
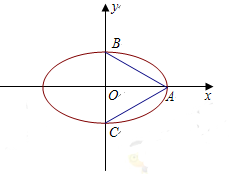
设椭圆E的方程为 ,点O为坐标原点,点A的坐标为
,点O为坐标原点,点A的坐标为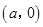 ,点B的坐标为
,点B的坐标为 ,点M在线段AB上,满足
,点M在线段AB上,满足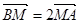 ,直线OM的斜率为
,直线OM的斜率为 .
.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为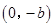 ,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为 ,求E的方程.
,求E的方程.
已知函数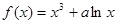
(Ⅰ)当 时,求曲线
时,求曲线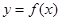 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当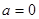 时,求曲线
时,求曲线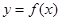 过点
过点 处的切线方程.
处的切线方程.
设函数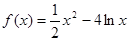
(Ⅰ)求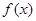 的单调区间;
的单调区间;
(Ⅱ)求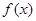 在区间
在区间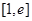 上的最值.
上的最值.
已知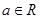 ,命题
,命题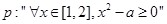 ,命题
,命题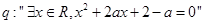 .
.
(Ⅰ)若命题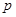 为真命题,求实数
为真命题,求实数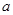 的取值范围;
的取值范围;
(Ⅱ)若命题 为假命题,求实数
为假命题,求实数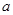 的取值范围.
的取值范围.