(本小题满分10分)(注意:在试题卷上作答无效)
在△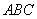 中,角
中,角 、
、 、
、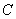 所对的边分别为
所对的边分别为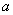 、
、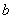 、
、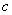 ,且
,且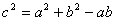 .
.
(Ⅰ)若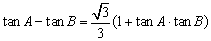 ,求角
,求角 ;
;
(Ⅱ)设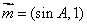 ,
,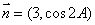 ,试求
,试求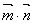 的最大值.
的最大值.
(本小题满分13分)已知函数
(I)若函数 在
在 时取到极值,求实数
时取到极值,求实数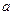 的值;
的值;
(II)试讨论函数 的单调性;
的单调性;
(III)当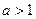 时,在曲线
时,在曲线 上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求
上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求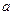 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分13分)海岛B上有一座为10米的塔,塔顶的一个观测站A,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D处。(假设游船匀速行驶)
(I)求该船行使的速度(单位:米/分钟)
(II)又经过一段时间后,油船到达海岛B的正西方向E处,问此时游船距离海岛B多远。
(本小题满分13分)已知定义域为R的函数 是奇函数.
是奇函数.
(I)求a的值,并指出函数 的单调性(不必说明单调性理由);
的单调性(不必说明单调性理由);
(II)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分13分) 在平面直角坐标系 中,O为坐标原点,已知点A
中,O为坐标原点,已知点A
(I)若 求证:
求证: ;
;
(II)若 求
求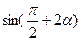 的值.
的值.
(本小题满分14分)
已知数列 满足
满足 且
且
(Ⅰ)求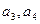 ;
;
(Ⅱ)求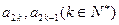 ;
;
(Ⅲ)设 为非零整数),试确定
为非零整数),试确定 的值,使得对任意
的值,使得对任意 都有
都有 成立。
成立。