求下列标准方程
(1)椭圆的两个焦点坐标分别为(0,2),(0,-2),且点P( ,
, )在椭圆上.
)在椭圆上.
(2)椭圆长轴是 短轴的3倍,且过点A(4,0).
短轴的3倍,且过点A(4,0).
(3)双曲线经过点(-3,2),且一条渐近线为y= x.
x.
(4)双曲线离心率为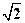 ,且过点(4,
,且过点(4, ).
).
(本小题满分12分)
已知数列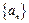 是公差不为零的等差数列,且
是公差不为零的等差数列,且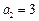 ,又
,又 成等比数列.
成等比数列.
(Ⅰ)求数列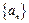 的通项公式;
的通项公式;
(Ⅱ)设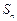 为数列
为数列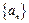 的前
的前 项和,求使
项和,求使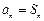 成立的所有
成立的所有 的值.
的值.
(本题满分14分) 设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若 ,求
,求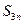 的值;
的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式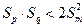 成立;
成立;
(3)是否存在常数k和等差数列{an},使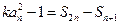 恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
(本题满分13分) 已知函数 ,数列
,数列 满足
满足 ,
, .
.
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)求 ;
;
(Ⅲ)求证:
(本题满分13分) 已知函数 ,
, .
.
(1)当 时,若
时,若 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对 :存在
:存在 ,使得
,使得 的最大值,
的最大值, 的最小值;
的最小值;
(本题满分13分已知数列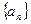 是公比为
是公比为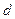
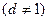 的等比数列,且
的等比数列,且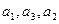 成等差数列.
成等差数列.
(Ⅰ) 求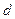 的值;
的值;
(Ⅱ) 设数列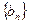 是以2为首项,
是以2为首项,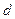 为公差的等差数列,其前
为公差的等差数列,其前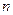 项和为
项和为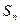 ,
,
试比较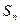 与
与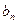 的大小.
的大小.